Casastrangers to friends

Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers

Por um escritor misterioso
Last updated 16 novembro 2024
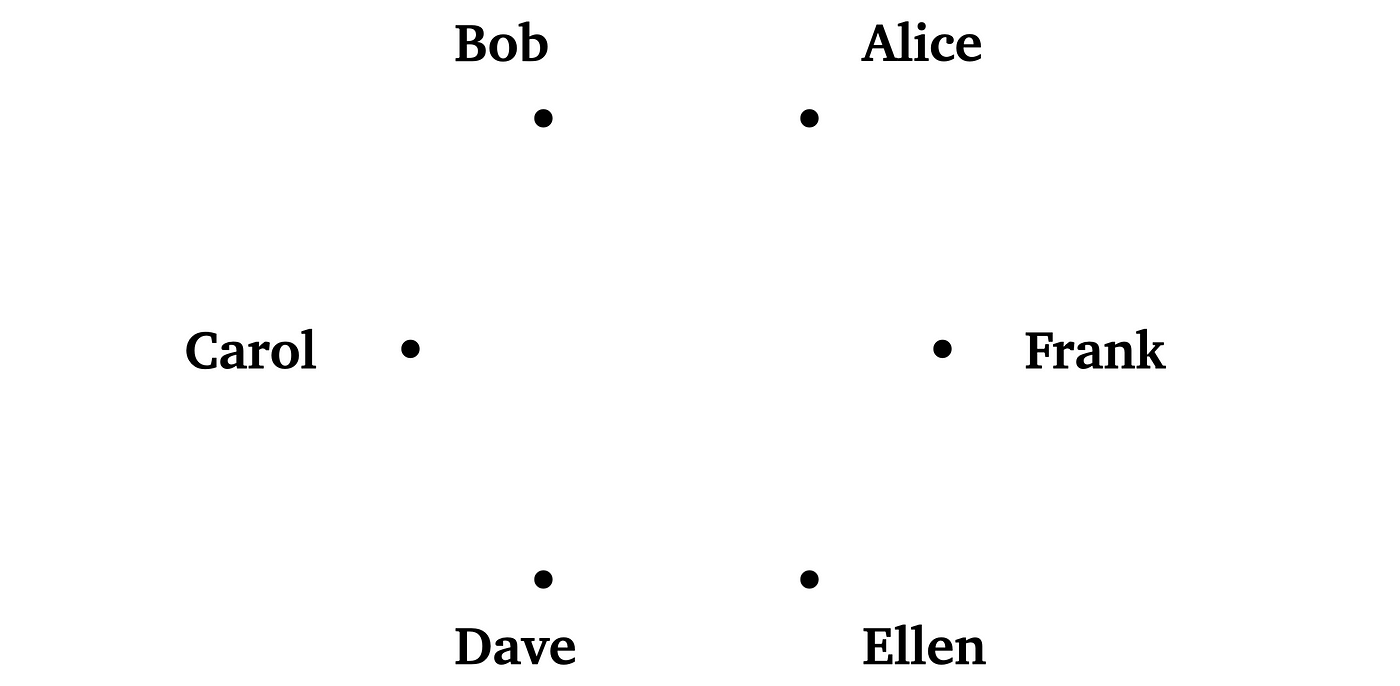
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Let’s take a look at Alice first. To her, each one of the other five (Bob, Carol, Dave, Ellen, and Frank) is either a friend or a stranger. Suppose Bob, Dave, and Frank are friends to Alice, and…
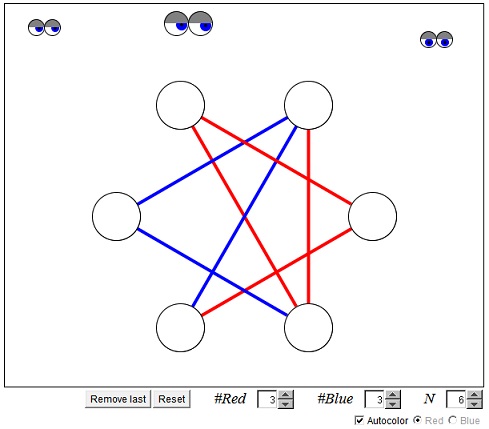
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Friends and strangers
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Party Acquaintances
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Can Math Prove You'll Always Be the Odd One Out At Parties?, by Mary Paskhaver, Geek Culture
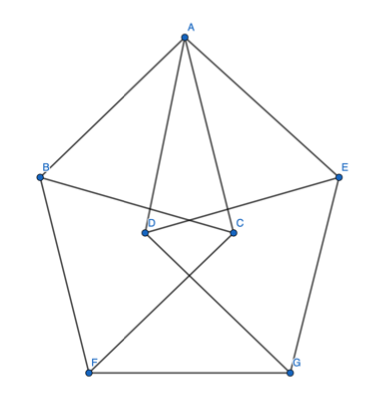
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Ramsey Theorems in Euclidean Geometry — Math In Action
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
How to prove: at a party of six people either there are three mutual acquaintances or there are three mutual strangers - Quora
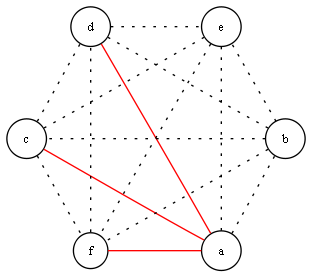
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Friends and Strangers
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
SOLVED: Prove this theorem: Among any six people, there exists a group of 3 mutual friends or a group of 3 mutual strangers. (Here friends and strangers are considered symmetric relations, i.e.
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Solved Counting: product rule, sum rule, inclusion-exclusion
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Friendship - Wikipedia
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
The Mathematical Tourist: February 2021
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Solved 4. Prove that in any group of 6 people there are
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Correlation, Causation, and Ramsey Theory
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Ramsey's Theorem: Friends and Strangers
Recomendado para você
você pode gostar

© 2014-2024 tokoonline2.msd.biz.id. All rights reserved.